Математическая модель двигателя постоянного тока

Отметим, что предлагается использовать регулирование скорости вращения двигателя по цепи якоря. Для ДПТ в этом случае вводится линеаризованная модель, структурная схема которой представлена на рисунке 3.2.

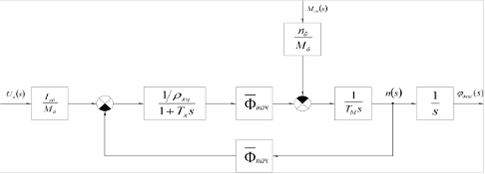
Рисунок 3.2 - Линеаризованная модель ДПТ

Здесь и далее под базовыми параметрами двигателя будем понимать номинальные значения.

Для расчета параметров модели воспользуемся таблицей 2.3 и 2.4. Обратное значение относительного сопротивления якорной цепи равно

.

Интересующие нас отношения схемы 3.2 будут равны

,

Рабочее значение магнитного потока выбирается в промежутке , но в большинстве случаев достаточно задаться . Тогда .

Постоянная времени якорной цепи Tяц приведена в паспортных данных ДПТ (таблица 2.3). Статический момент Мст, действующий на вал двигателя со стороны редуктора и нагрузки, будет равен (пользуемся таблицей 2.2)

.

Условимся, что этот статический момент действует при любом грузе для упрощения модели.

Последний оставшийся параметр - механическая постоянная двигателя - переменный и зависит от массы поднимаемого / опускаемого груза. Определим интервал, в котором данный параметр изменяется, воспользовавшись таблицами 2.2 и 2.3.

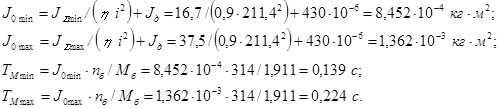
Таким образом, механическая постоянная двигателя изменяется в пределах

. (3.1)

Подставим рассчитанные параметры в структурную схему рисунка 3.2.

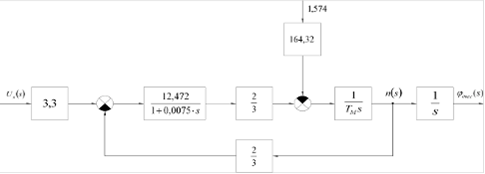
Рисунок 3.3 - Линеаризованная модель ДПТ с подставленными параметрами

Для дальнейшего синтеза нам понадобится передаточная функция модели двигателя, однако, очевидно, что модель двигателя обладает переменной структурой. Тем не менее, колебания параметра происходит в не очень широких пределах, поэтому нам достаточно рассмотреть два краевых случая: при максимальной массе груза и при минимальной.

Если сворачивать структурную схему в общем виде, пока не обращая внимания на самый правый интегратор (см. рисунок 3.2), то передаточная функция представится в следующем виде

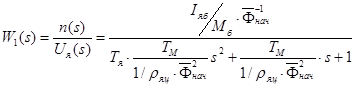. (3.2)

Подставив известные параметры, с учетом переменной структуры (3.1), мы получаем две передаточные функции двигателя

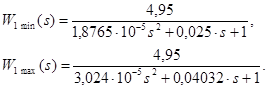(3.3)

Убедимся, что передаточные функции представляют типовые колебательные звенья, для чего достаточно узнать значение коэффициента демпфирования.

Очевидно, что коэффициенты демпфирования больше единицы, а значит, двигатель не является колебательным звеном. В этом случае передаточная функция может быть представлена в виде произведения двух апериодических звеньев.

Свернув полиномы знаменателей (3.3) через теорему Виета получим

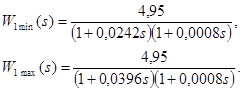(3.4)

Теперь учтем самый правый интегратор в схеме рисунка 3.3 и получим окончательную передаточную функцию модели двигателя. С учетом (3.4) запишем

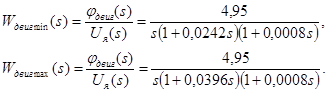(3.5)

Другие стьтьи в тему

Разработка рекомендаций по повышению безопасности мобильных платежей
мобильный телефон платеж безопасность Оплата за товары и услуги с помощью мобильных устройств уже перестала быть экзотикой, а мобильные платежи, являющиеся ключевой составляющей мобильных финансовых услуг, набирают обороты во всем мире. Но вместе с тем растет риск быть обманутыми злоу ...

Разработка узкополосного частотно-модулированного приемника
Радиосистемы различного назначения, от простейших радиотелефонов до компьютерных радиосетей, пользуются всё большим успехом у пользователей во всём мире. После нескольких десятилетий развития теории и техники радиосистем значительно выросли скорость и качество коммуникационных услуг п ...