Демодулятор

Демодулятор, оптимальный по критерию максимального правдоподобия в канале с аддитивной белой гауссовской помехой, осуществляет некогерентную обработку наблюдаемой смеси

И принимает решение о значении , полученного кодового символа.

Выход демодулятора одновременно представляет собой выход дискретного канала.

6.1 Запишем правило работы решающей схемы демодулятора, оптимального по критерию максимального правдоподобия.

Правило решения по критерию идеального наблюдателя ( Критерий Котельникова) имеет следующий вид:

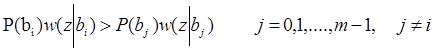
Приемник реализующий этот алгоритм называется приемником Котельникова.

Для двоичной системы правило это сводится к проверке неравенства:

( 6.1 )

При выполнении которого регистрируется символ 1, а при невыполнении 0.

Правило можно записать иначе. Решение о том, что передавался символ bi должно приниматься, если для всех i≠j выполняется m-1 неравенств

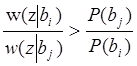( 6.2 )

Отношение в левой части этого неравенства называется отношением правдоподобия двух гипотез: о том, что передавался символ bi, и о том, что передавался символ bj. Его обозначают Λij.

Так как все символы передаются равновероятно правило (6.2) упрощается

Λij > 1 (6.3)

Иногда вводят в рассмотрение помимо m гипотез о передачи символов еще дополнительную "шумовую" гипотезу о том, что никакой сигнал не передавался. Отношение правдоподобия 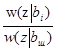= Λiш обычно обозначается просто Λi. Тогда правило (6.3) можно записать так:

Λi >Λj при i≠j (6.4)

Это правило максимума правдоподобия для случая, когда все символы передаются равновероятно.

Для двоичной системы правило (6.4) сводится к проверке неравенством:

Λ1 >Λ0 (6.5)

Нам дан оптимальный некогерентный прием.

Для двоичной системы сигналов правило оптимального некогерентного приема выражается неравенством:

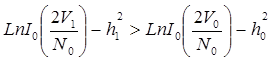( 6.6 )

При выполнении этого неравенства регистрируется единица, в противном случаи ноль.

6.2 Запишем алгоритм работы и начертим структурную схему оптимального демодулятора для относительной фазовой модуляции с оптимальным некогерентным приемом.

Для двоичной системы сигналов правило оптимального некогерентного приема выражается неравенством:

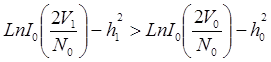
При выполнении этого неравенства регистрируется единица, в противном случаи ноль.

Можно записать:

Vi>Vj j≠i

Для двоичных систем это правило сводится к проверке одного неравенства

V1>V0 ( 6.7 )

Где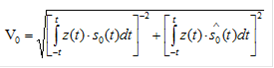

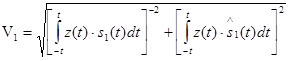
Поскольку при ОФМ информационный параметр сигнала определяется между двумя соседними элементами ( на интервале от -Т до Т), то оптимальный алгоритм можно записать

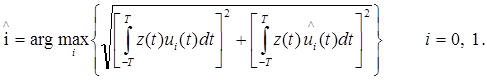( 6.8 )

Приходящий согнал s(t) на двух тактовых интервалах при ОФМ можно представить в зависимости от символа, передаваемого n-м элементом, так:

(при передаче символа 1)

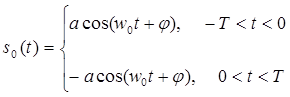(при передаче символа 0) ( 6.9 )

Где φ - случайная начальная фаза, неизвестная при приеме, зависящая, в частности, от символа, передававшегося (n-2)-м элементом.

Другие стьтьи в тему

Расчёт трассы прокладки волоконно-оптического кабеля между населёнными пунктами
В современном мире быстрыми темпами наращиваются объёмы информации, соответственно повышаются требования к передающей аппаратуре, поскольку каждые пять-шесть лет объём передаваемой информации увеличивается вдвое. Задача передачи такого количества информации с высокой степенью дост ...

Разработка проекта сети доступа по технологии GPON микрорайона №5 г. Минусинска
Тенденция развития телекоммуникационной сети начала ХХI века должна отвечать времени, то есть быть высокоорганизованной, интеллектуальной, автоматизированной, соответствовать техническому уровню высокоразвитых стран мира, обеспечивать передачу разнообразных сообщений и предоставление ...