Алгоритм обработки информации в приемном блоке

Еще одним распространенным критерием является критерий максимального правдоподобия.

Приведенная выше функция распределения n случайных значений напряжения на выходе приемника W(u1, u2, u3, .un) называется функцией правдоподобия. Существует метод максимального правдоподобия, который позволяет находить максимум этой функции. Для этого производная функции правдоподобия по искомому сигналу приравнивается нулю. Решение полученного уравнения позволяет найти максимально правдоподобную оценку значения сигнала. Так, например, если случайные напряжения на выходе приемника u1, u2, u3, .un распределены по нормальному закону, то эта оценка совпадает с их средним значением. Метод позволяет получить оценки с наименьшим (относительно других методов) значением дисперсии. Такие оценки называются эффективными. Таким образом, критерием оптимальности процедуры, осуществляемой по методу максимального правдоподобия, является эффективность оценки. При использовании критерия максимального правдоподобия решение о наличии сигнала принимается в том случае, когда функция правдоподобия W1 превосходит функцию правдоподобия W0:

.

Как уже указывалось выше, некоторые априорные вероятности, необходимые для принятия решения о наличии цели, на практике обычно неизвестны. Поэтому наиболее широко используется еще один критерий, не зависящий от этих вероятностей. Это критерий Неймана-Пирсона, который обеспечивает максимальную вероятность правильного обнаружения P(A1+A'1) (в дальнейшем обозначается D) при заданной вероятности ложной тревоги P(A0+A'1) (в дальнейшем обозначается F). В соответствии с этим критерием величина порога u0 в правой части отношения правдоподобия выбирается из заданной условной вероятности ложной тревоги:

. (3.11)

Таким образом, решение задачи обнаружения цели в большинстве случаев сводится к вычислению отношения [26]:

, (3.12)

которое называется отношением правдоподобия. Решение о наличии цели принимается в том случае, когда это отношение превосходит некоторый фиксированный уровень u0, установленный заранее в зависимости от принятого критерия.

Традиционные методы оптимального обнаружения сигналов тревог используют в качестве априорной информации функцию распределения вероятностей напряжения шума на выходе приемника. Этот шум обычно аппроксимируется, так называемым, «белым шумом», имеющим равномерную спектральную плотность мощности N0 Вт/Гц в полосе частот приемника ∆f и нормальную функцию распределения напряжения во времени [25]:

. (3.13)

Эта функция распределения имеет нулевое среднее значение и дисперсию σ2 = N0-∆f. Отсчеты напряжения шума, отстоящие друг от друга на интервал ∆t = 1/2∆f являются статистически независимыми. Тогда функция правдоподобия для N отсчетов напряжения шума является произведением N сомножителей:

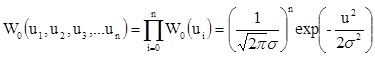. (3.14)

Функция распределения суммы сигнала и шума зависит от структуры сигнала. Для понимания общих закономерностей оптимальной обработки в традиционной теории обычно используется гипотетический сигнал, параметры которого полностью известны за исключением времени его прихода. В этом случае функция распределения суммы сигнала и шума отличается от функции распределения шума только тем, что среднее значение этой суммы отлично от нуля и равно амплитуде сигнала s:

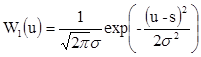. (3.15)

Функция правдоподобия суммы сигнала и шума будет равна:

.(3.16)

Другие стьтьи в тему

Расчет параметров выпрямительно-инверторного преобразователя, выполненного по шестипульсовой мостовой схеме
Трёхфазный мостовой выпрямительно-инверторный преобразователь (ВИП) питается от сети с номинальным напряжением UС=U1Л и заданными пределами колебания этого напряжения %UС Известна мощность короткого замыкания SКЗ, характеризующая реактанс связи точки подключения ВИП и шин бесконечной ...

Разработка комплекта конструкторских документов на стабилизатор напряжения
При проектировании, ремонте, производстве, эксплуатации, испытаниях электронных и электротехнических узлов электротехнического оборудования используется техническая документация, которая называется конструкторской. Для облегчения проектирования и разработки конструкторской документаци ...