Цифровые системы автоматического регулирования

Поскольку выходной сигнал АЦП представляет собой последовательность импульсов с амплитудами y(kT), то его можно описать выражением:

,

где предполагается, что сигнал y(t) существует для t > 0.

Преобразовав это выражение по Лапласу, получим:

.

Рис. 9. Одноконтурная цифровая система управления

Если ввести переменную , можно определить новое преобразование, называемое z - преобразованием:

.

Для простых случаев изображение Y(z) легко найти по определению. Пусть

y[k]=δ[k] = 1 - единичный дискретный импульс, тогда

.

Далее в качестве примера рассмотрим дискретный единичный ступенчатый сигнал (рис. 10):

Рис. 10. Единичная ступенчатая функция.

При , соответствующий ряд сходится и представляет собой сумму бесконечно убывающей геометрической прогрессии, которая вычисляется в замкнутом виде:

.

В теории дискретных систем используются также операторы обратного и прямого сдвига на один такт.

Оператор обратного сдвига (z-1) позволяет получить предыдущий элемент последовательности {e[k]}:

z-1e[k] = e[k-1], или .

Этот оператор соответствует запаздыванию на один такт и является физически реализуемым в том смысле, что его применение не дает будущих значений сигнала. Для того, чтобы найти остальные предшествующие элементы последовательности, надо применить оператор обратного сдвига несколько раз:

z-me[k] = e[k-m].

Если найти z - преобразование для входного Y(z) и выходного U(z) сигналов системы, то можно найти передаточную функцию системы в z - области:

.

Реализация цифровых регуляторов

Рассмотрим непрерывный ПИД-регулятор с передаточной функцией:

.

Цифровую реализацию этого регулятора можно получить, если использовать дискретную аппроксимацию операций дифференцирования и интегрирования.

Для производной по времени используется правило обратной разности:

.

Применив к этому выражению z - преобразование, получим:

.

Операцию интегрирования можно аппроксимировать с помощью формулы прямоугольников:

,

где u(kT) - выходной сигнал интегрирующего звена в момент времени

t= kT.

Применив к этому выражению z - преобразование, получим:

,

откуда передаточная функция интегрирующего звена:

.

Таким образом, передаточная функция цифрового ПИД-регулятора имеет вид:

.

Или для регулятора со взаимозависимыми настройками:

.

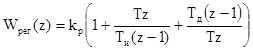Поскольку в большинстве случаев объект является устройством непрерывного типа, то для того, чтобы смоделировать переходные процессы в исследуемой системе необходимо либо объект представить в цифровой форме, либо получить эквивалентную передаточную функцию регулятора, отвечающую цифровой реализации его алгоритма. Для этого проводится замена и добавляется передаточная функция демодулятора.

Другие стьтьи в тему

Разработка вычислительного блока системы электромагнитного позиционирования
Актуальность развития методов точного определения координат и углов ориентации того или иного объекта по отношению к некоторой заданной системе координат трудно переоценить. Определение пространственных и угловых координат движущихся объектов лежит в основе решения многих важных нау ...

Регулируемый реверсивный тиристорный электропривод постоянного тока
В данном курсовом проекте рассматривается регулируемый электропривод. Регулируемым называется электропривод, который обеспечивает с заданной точностью движение исполнительного органа рабочей машины в соответствии с произвольно изменяющимся входным сигналом управления. Этот сигнал може ...