Разрешение по дальности

Критерий Вудворда: положим, что имеются две неподвижные точечные цели, отличающиеся только по дальности. Т.к. доплеровский сдвиг отсутствует, то эти сигналы можно записать в виде:

и

где: - начало отсчета времени, соответствующее моменту излучения зондирующего импульса; - время запаздывания сигнала от первой цели; - время запаздывания сигнала второй цели, относительно сигнала первой.

Без потери общности можно положить . Требуется найти меру различимости этих сигналов. В методе, предлагаемом Вудвордом, средний квадрат отклонения и :

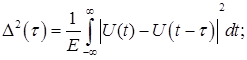
Для большей разрешающей способности средний квадрат должен быть как можно больше для всех в априорном интервале задержек, за исключением малого интервала около точки :

;

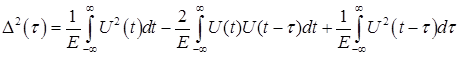Т.к. первый и последний интегралы дают энергию сигнала, то сумма их равна 2, следовательно:

;

где: 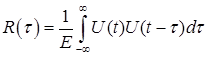- нормированная АКФ сигнала.

Таким образом, мерой разрешающей способности по критерию Вудворда, является АКФ сигнала.

Чтобы различие сигналов было большим, нужно выбирать сигнал такой формы, чтобы был как можно ближе к нулю, за исключением окрестности точки.

Часто в задачах разрешения используют понятие функции неопределенности.

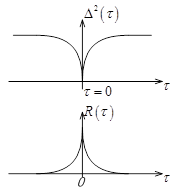
В данном случае функция неопределенности представляет собой . Максимальное значение получает при Если для некоторого , то две цели, сигналы от которых отличаются этим запаздыванием, будут совершенно неразличимы. Если близка к при некотором , тогда две цели, отличающиеся запаздыванием, могут быть разделены, но это связано с большими трудностями.

Идеальная форма - это - функция. Но это невозможно реализовать физически.

Видно, что выражение для отклика СФ с точностью до некоторого множителя совпадает с АКФ сигнала. Таким образом, разрешающая способность по времени тем выше, чем меньше длительность отклика СФ. При обнаружении сигнала со случайной фазой, ее влияние исключают с помощью детектора. При этом отклик СФ на выходе линейного детектора описывается модулем комплексной огибающей корреляционной функции , а на выходе квадратичного детектора - квадратом модуля . Для произвольного сигнала имеет вид:

Другие стьтьи в тему

Расчет параметров выпрямительно-инверторного преобразователя, выполненного по шестипульсовой мостовой схеме
Трёхфазный мостовой выпрямительно-инверторный преобразователь (ВИП) питается от сети с номинальным напряжением UС=U1Л и заданными пределами колебания этого напряжения %UС Известна мощность короткого замыкания SКЗ, характеризующая реактанс связи точки подключения ВИП и шин бесконечной ...

Расчет и конструирование схемы параллельного регистра на триггере CLD - типа
Одним из основных достижений микроэлектроники является создание на основе фундаментальных и прикладных наук новой элементной базы - интегральных микросхем. Развитие вопросов проектирования и совершенствование технологии позволило в короткий срок создать высокоинтегрированные функциона ...