Расчет параметров цифрового фильтра

Обратное z-преобразование

Обратное z-преобразование (z-1) позволяет восстанавливать последовательность дискретного времени х(п) по ее z-образу. z-1 особенно полезно в операциях ЦОС, например, при поиске импульсной характеристики цифровых фильтров. В символической форме обратное z-преобразование можно определить как:

(n) = Z-1[X(z)],

где X(z) - это z-образ последовательности x(n), а Z-1 - символ, обозначающий обратное z-преобразование.

Предположив, что последовательность причинна, z-образ X(z) можно разложить в степенной ряд как:

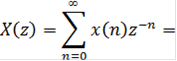
Видно, что значения последовательности х(n) - это коэффициенты z-n (n = 0,1, .), и поэтому их можно найти непосредственно. На практике X(z) часто выражается через отношение двух многочленов от z-1 или, что эквивалентно, от z:

В этом виде обратное z-преобразование x(n) можно найти с помощью одного из многих методов, например:

а) метода разложения в степенной ряд;

б) метода разложения на элементарные дроби;

У каждого метода есть свои преимущества и недостатки. С точки зрения математической строгости метод вычетов, возможно, самый элегантный. Однако метод степенных рядов лучше всего подходит для компьютерных расчетов.

Метод степенных рядов

Если дано z-преобразование X(z) причинной последовательности, то его можно разложить в бесконечный ряд относительно z-1 или z путем деления в столбик (иногда его называют синтетическим делением):

=

В этом методе числитель и знаменатель функции X(z) сперва выражаются либо через уменьшающийся показатель степени z, либо через увеличивающейся показатель степени z-1, а затем путем деления в столбик находится частное.

Метод разложения на элементарные дроби

В этом методе z-преобразование вначале раскладывается на сумму простых дробей. Затем по таблицам, подобным (смотреть в приложении) находится обратное z-преобразование каждой элементарной дроби. Эти образы суммируются, и получается общее обратное z-преобразование. На практике во многих случаях z-преобразование задается как отношение многочленов по z или z-1 и имеет уже знакомый вид

=

(1)

Если полюсы функции X(z) - первого порядка и N - М, то X(z) можно разложить как:

(2)

где pk - полюсы функции X(z), Ck - коэффициенты элементарных дробей, a

= bN/aN.

Сk также называют вычетами функции X(z).

Если в уравнении (1) порядок числителя меньше, чем порядок знаменателя, т.е. N < М, то В0 будет равно нулю. Если N > М, то X(z) вначале нужно сократить, чтобы получить N < М, путем деления в столбик многочленов числителя и знаменателя, записанных через уменьшающийся показатель степени z-1. Остаток можно выразить так, как это сделано в уравнении (2).

Другие стьтьи в тему

Разработка технологической инструкции по обслуживанию и ремонту импульсной паяльной системы
Прохождение производственной практики позволяет практиканту закрепить теоретические знания, опробовав их на деле. Главной особенностью данной практики является то, что практикант имеет хорошую возможность для усовершенствования собственных навыков владения рабочим инструментом, а так ...

Разработка приемника системы персонального радиовызова
Системы персонального радиовызова позволяют передавать вызов и необходимый минимум информации одному человеку или группе людей независимо от места их нахождения. Первоначально системы персонального радиовызова функционировали с радиусом действия, ограниченным территорией или помещения ...